Cassini and Catalan identities

Cassini's identity and Catalan's identity are mathematical identities for the Fibonacci numbers. The former is a special case of the latter, and states that for the nth Fibonacci number,

F_{n-1}F_{n%2B1} - F_n^2 = (-1)^n.\,

Catalan's identity generalizes this:

F_n^2 - F_{n-r}F_{n%2Br} = (-1)^{n-r}F_r^2.\,

Contents

History

Cassini's formula was discovered in 1680 by Jean-Dominique Cassini, then director of the Paris Observatory, and independently proven by Robert Simson (1753). Eugène Charles Catalan found the identity named after him in 1879.

Proof by matrix theory

A quick proof of Cassini's identity may be given by recognising the left side of the equation as a determinant of a 2×2 matrix of Fibonacci numbers. The result is almost immediate when the matrix is seen to be the nth power of a matrix with determinant −1:

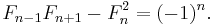
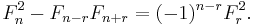
F_{n-1}F_{n%2B1} - F_n^2 =\det\left[\begin{matrix}F_{n%2B1}&F_n\\F_n&F_{n-1}\end{matrix}\right] =\det\left[\begin{matrix}1&1\\1&0\end{matrix}\right]^n =\left(\det\left[\begin{matrix}1&1\\1&0\end{matrix}\right]\right)^n =(-1)^n.

References

External links